Stereometria. Płaszczyzny prostopadłe, warunek prostopadłości płaszczyzn Jeżeli płaszczyzna jest prostopadła do jednego z dwóch równoległych

Nazywa się dwie płaszczyzny, które się przecinają prostopadły, jeżeli trzecia płaszczyzna, prostopadła do linii przecięcia tych dwóch płaszczyzn, przecina je wzdłuż linii prostopadłych (patrz rysunek).

Dowolna płaszczyzna prostopadła do linii przecięcia płaszczyzn prostopadłych przecina je wzdłuż linii prostopadłych.

Znak prostopadłości płaszczyzn

Twierdzenie 1. Jeżeli płaszczyzna przechodzi przez linię prostopadłą do innej płaszczyzny, wówczas płaszczyzny te są prostopadłe (patrz rysunek).

Twierdzenie 2. Jeżeli prosta leżąca w jednej z dwóch prostopadłych płaszczyzn jest prostopadła do linii ich przecięcia, to jest także prostopadła do drugiej płaszczyzny (patrz rysunek).

Przykład zastosowania twierdzenia 2
Niech istnieją dwie prostopadłe płaszczyzny, które przecinają się na linii prostej A(widzieć zdjęcie). Znajdź odległość od punktu A, co leży w płaszczyźnie i nie leży w płaszczyźnie, płaszczyzna.

W płaszczyźnie konstruujemy prostopadłą do A przez punkt A. Pozwól mu przejść A w tym punkcie B. AB- wymagana odległość.
Zwróć na to uwagę.
1. Przez punkt znajdujący się poza płaszczyzną można poprowadzić wiele płaszczyzn prostopadłych do tej płaszczyzny (patrz rysunek). (Ale wszystkie przejdą przez linię prostą prostopadłą do tej płaszczyzny, która przechodzi przez dany punkt.)

2. Jeżeli płaszczyzna jest prostopadła do danej płaszczyzny, nie oznacza to, że jest ona prostopadła do dowolnej prostej równoległej do tej płaszczyzny.
Na przykład na poniższym rysunku i przecinają się w linii prostej B, I A wchodzi do jednego z samolotów i . Dlatego prosto A jednocześnie równolegle do dwóch prostopadłych płaszczyzn.

Prostopadłość płaszczyzn Definicja. Dwie płaszczyzny nazywamy prostopadłymi, jeśli kąt liniowy na krawędzi kąta dwuściennego między tymi płaszczyznami jest linią prostą.
Podpisać prostopadłość płaszczyzn. Jeżeli płaszczyzna przechodzi przez linię prostopadłą do innej płaszczyzny, to płaszczyzny te są prostopadłe.
Dowód. Pozwalać A I ? - dwie przecinające się płaszczyzny, Z- linia ich przecięcia i A- prosty prostopadle do płaszczyzny? i leżeć w samolocieA. A - punkt przecięcia liniiA I Z. W samolocie? z punktu I przywrócimy prostopadłą i niech to będzie linia prosta. B A Prosty samolot? , co oznacza, że ​​jest prostopadła do dowolnej linii prostej w tej płaszczyźnie, czyli linii prostych prostopadłą i niech to będzie linia prosta I Zprostopadły . Kąt pomiędzy liniami prostymi A I B - płaszczyzny liniowe A I ? i jest równy 90°, więc Jak prosty A prostopadle do linii prostejprostopadłą i niech to będzie linia prosta(sprawdzone).Z definicji płaszczyznyA I ? prostopadły.

Twierdzenie 1. Jeżeli z punktu należącego do jednej z dwóch prostopadłych płaszczyzn narysuj prostopadła do innej płaszczyzny, wówczas prostopadła ta leży całkowicie w pierwszej płaszczyźnie.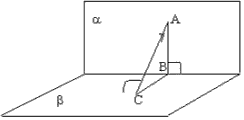
Dowód. Pozwalać A I ? - prostopadle do płaszczyzny i Z - linia prosta ich przecięcia, A - punkt leżeć płasko A i nienależące bezpośrednio do Z. Niech prostopadle do płaszczyzny? poprowadzona z punktu A nie leży na płaszczyźnie A, to punkt C jest podstawą ta prostopadła leży w samolot? Z. i nie należy do linii Z punktu A obniżamy prostopadłą AB Z. bezpośrednioLinia AB jest prostopadłapłaszczyzna (używam Twierdzenia 2).Przez prostą AB i punkt C Narysujemy samolot? (prosta i punkt definiują płaszczyznę i tylko jedną). Widzimy to w ? samolot z jednego punktu A do prostej BC poprowadzono dwie prostopadłe, co nie może mieć miejsca, czyli linię AC A.

pokrywa się z prostą AB, a prosta AB z kolei leży całkowicie na płaszczyźnie. Twierdzenie 2Jeśli w jednej z dwóch prostopadłych płaszczyzn narysujemy prostopadłą do ich linii
Dowód. Pozwalać A przecięcia, to ta prostopadła będzie prostopadła do drugiej płaszczyzny. Z - I ? - dwie prostopadłe płaszczyzny, linia ich przecięcia i A - prosty Z i leżeć w samolocieAprostopadle do linii prostej A I Z.. A - punkt przecięcia linii W samolocie ? z punktu A przywracamy prostopadłą i niech będzie to linia prostaB. A Iprostopadłą i niech to będzie linia prosta Kąt pomiędzy liniami prostymi - liniowy kąt na krawędzi kąta dwuściennego pomiędzy A samoloty I ?A i jest równy 90°, ponieważ płaszczyzna I ? A prostopadły. Prostyprostopadłą i niech to będzie linia prostaprostopadle do linii prostej Z(według sprawdzonych) i bezpośrednich według warunku. A Więc to jest proste

prostopadle do płaszczyzny? (

Rozważana jest zależność prostopadłości płaszczyzn – jedna z najważniejszych i najczęściej stosowanych w geometrii przestrzeni i jej zastosowaniach.

Ze wszystkich różnorodnych wzajemnych ustaleń

Na szczególną uwagę i badanie zasługują dwie płaszczyzny, gdy płaszczyzny są do siebie prostopadłe (na przykład płaszczyzny sąsiednich ścian pomieszczenia,

Powyższe przykłady pozwalają nam zobaczyć jedną z głównych właściwości badanej relacji - symetrię położenia każdej płaszczyzny względem drugiej. Symetrię zapewnia fakt, że płaszczyzny sprawiają wrażenie „utkanych” z prostopadłych. Spróbujmy wyjaśnić te obserwacje.

Miejmy na niej płaszczyznę α i linię prostą c (ryc. 418, a). Przeprowadźmy przez każdy punkt linii c proste prostopadłe do płaszczyzny α. Wszystkie te linie są do siebie równoległe (dlaczego?) i na podstawie Zadania 1 § 8 tworzą pewną płaszczyznę β (ryc. 418, b). Naturalne jest nazywanie płaszczyzny β prostopadły płaszczyzna α.

Z kolei wszystkie linie leżące w płaszczyźnie α i prostopadłe do linii c tworzą płaszczyznę α i są prostopadłe do płaszczyzny β (ryc. 418, c). Rzeczywiście, jeśli a jest dowolną linią, to przecina linię c w pewnym punkcie M. Linia b prostopadła do α przechodzi przez punkt M na płaszczyźnie β, zatem b a. Zatem a c, a b, zatem a β. Zatem płaszczyzna α jest prostopadła do płaszczyzny β, a linia prosta c jest linią ich przecięcia.

Dwie płaszczyzny nazywamy prostopadłymi, jeśli każdą z nich tworzą proste prostopadłe do drugiej płaszczyzny i przechodzące przez punkty przecięcia tych płaszczyzn.

Prostopadłość płaszczyzn α i β jest oznaczona znanym znakiem: α β.

Jedną z ilustracji tej definicji można sobie wyobrazić, jeśli weźmiemy pod uwagę fragment pokoju w wiejskim domu (ryc. 419). W nim podłoga i ściana są wykonane z desek prostopadłych odpowiednio do ściany i podłogi. Dlatego są prostopadłe. Na praktyce

oznacza to, że podłoga jest pozioma, a ściana pionowa.

Powyższa definicja jest trudna w zastosowaniu podczas faktycznego sprawdzania prostopadłości płaszczyzn. Ale jeśli dokładnie przeanalizujemy rozumowanie, które doprowadziło do tej definicji, zobaczymy, że prostopadłość płaszczyzn α i β została zapewniona przez obecność w płaszczyźnie β linii prostej b prostopadłej do płaszczyzny α (ryc. 418, c) . Doszliśmy do najczęściej stosowanego w praktyce kryterium prostopadłości dwóch płaszczyzn.

406 Prostopadłość prostych i płaszczyzn

Twierdzenie 1 (test na prostopadłość płaszczyzn).

Jeżeli jedna z dwóch płaszczyzn przechodzi przez linię prostopadłą do drugiej płaszczyzny, to płaszczyzny te są prostopadłe.

 Niech płaszczyzna β przechodzi przez linię b prostopadłą do płaszczyzny α i c - linię przecięcia płaszczyzn α i β (ryc. 420, a). Wszystkie linie proste płaszczyzny β, równoległe do prostej b i przecinające prostą c, wraz z prostą b tworzą płaszczyznę β. Z twierdzenia o dwóch prostych równoległych, z których jedna jest prostopadła do płaszczyzny (Twierdzenie 1 § 19), wszystkie razem z prostą b są prostopadłe do płaszczyzny α. Oznacza to, że płaszczyzna β składa się z linii prostych przechodzących przez linię przecięcia płaszczyzn α i β i prostopadłych do płaszczyzny α (ryc. 420, b).

Teraz w płaszczyźnie α, przez punkt A przecięcia linii b i c, rysujemy linię a prostopadłą do linii c (ryc. 420, c). Linia prosta a jest prostopadła do płaszczyzny β, w oparciu o prostopadłość linii i płaszczyzny (ac, konstrukcyjnie, oraz b, ponieważ b α). Powtarzając poprzednie argumenty, stwierdzamy, że płaszczyzna α składa się z prostych prostopadłych do płaszczyzny β, przechodzących przez linię przecięcia płaszczyzn. Zgodnie z definicją płaszczyzny α i β są prostopadłe. ■

Ta funkcja umożliwia ustalenie prostopadłości płaszczyzn lub zapewnienie jej.

Przykład 1. Przymocuj osłonę do słupka tak, aby była ustawiona pionowo.

 Jeśli słupek stoi pionowo, wystarczy losowo przymocować do słupka osłonę i zabezpieczyć ją (ryc. 421, a). Zgodnie z cechą omówioną powyżej, płaszczyzna tarczy będzie prostopadła do powierzchni ziemi. W tym przypadku problem ma nieskończoną liczbę rozwiązań.

Prostopadłość płaszczyzn

Jeżeli słup stoi ukośnie do podłoża, wystarczy przymocować do słupa pionową szynę (ryc. 421, b), a następnie przymocować osłonę zarówno do szyny, jak i do słupa. W tym przypadku położenie tarczy będzie dość określone, ponieważ słupek i szyna wyznaczają jedną płaszczyznę. ■

W poprzednim przykładzie zadanie „techniczne” zostało zredukowane do zadania matematycznego polegającego na narysowaniu płaszczyzny prostopadłej do innej płaszczyzny przez daną linię prostą.

Przykład 2. Z wierzchołka A kwadratu ABCD wykreślono odcinek AK prostopadle do jego płaszczyzny, AB = AK = a.

1) Określ względne położenie płaszczyzn AKC i ABD,

AKD i ABK.

2) Skonstruuj płaszczyznę przechodzącą przez linię BD, prostopadłą do płaszczyzny ABC.

3) Narysuj płaszczyznę prostopadłą do płaszczyzny KAC przechodzącą przez środek F odcinka KC.

4) Znajdź obszar trójkąta BDF.

 Skonstruujmy rysunek odpowiadający warunkom z przykładu (ryc. 422).

1) Płaszczyzny AKC i ABD są prostopadłe zgodnie z warunkiem prostopadłości płaszczyzn (Twierdzenie 1): AK ABD , zgodnie z warunkiem. Płaszczyzny AKD i ABK są również prostopadłe

są biegunowe, w oparciu o prostopadłość płaszczyzn (Twierdzenie 1). Rzeczywiście, prosta AB, przez którą przechodzi płaszczyzna ABK, jest prostopadła do płaszczyzny AKD, zgodnie ze znakiem prostopadłości prostej i płaszczyzny (Twierdzenie 1 § 18): AB AD są jak sąsiednie boki kwadratu; AB AK, od

AK ABD.

2) Bazując na prostopadłości płaszczyzn, dla pożądanej konstrukcji wystarczy poprowadzić przez niektóre punkty prostą BD

408 Prostopadłość prostych i płaszczyzn

prosta prostopadła do płaszczyzny ABC. Aby to zrobić, wystarczy poprowadzić przez ten punkt linię równoległą do prostej AK.

Rzeczywiście, pod warunkiem, linia AK jest prostopadła do płaszczyzny ABC, a zatem zgodnie z twierdzeniem o dwóch liniach równoległych,

nasz, z czego jeden jest prostopadły do ​​płaszczyzny (Twierdzenie 1§19),

zbudowana prosta będzie prostopadła do płaszczyzny ABC.

Budowa.

Przez punkt

B prowadzimy

BYĆ,

równoległy

(ryc. 423). Pożądany jest samolot BDE.

3) Niech F będzie środkiem odcinka KC. Zawodowiec-

prowadzimy przez punkt

prostopadły-

samolot

Ta linia prosta

dzieci bezpośrednio

FO, gdzie

O - środek placu

ABCD (ryc. 424). Rzeczywiście, FO || AK

jak przeciętny

linia trójkąta

Ponieważ

prostopadły-

na powierzchni

bezpośrednie FO

gwizd-

det jest do niego prostopadła, zgodnie z twierdzeniem o

dwie równoległe linie, z których jedna

ry prostopadle do płaszczyzny (Twierdzenie 1

§ 19). Dlatego

FO DB. A ponieważ AC DB, to DB AOF (lub

KAC). Samolot

BDF przechodzi przez linię prostopadłą do

płaszczyzna KAC, czyli ta pożądana.

4) W trójkącie

Segment BDF FO

Wysokość dociągnięta

strona BD (patrz rys. 424). Mamy: BD =

2 a jako przekątna czworokąta

rata; FO = 1

AK =

1 a, z własności linii środkowej trójkąta.

Zatem S = 2 BD FO =

2 2 a

2 a =

. ■

Odpowiedź: 4)

2.

Badanie właściwości prostopadłości-

samolotów i ich zastosowań zacznijmy od najprostszego

to, ale bardzo przydatne twierdzenie.

Twierdzenie 2 (o prostopadłej do linii przecięcia płaszczyzn prostopadłych).

Jeżeli dwie płaszczyzny są prostopadłe, to prosta należąca do jednej płaszczyzny i prostopadła do przecięcia tych płaszczyzn jest prostopadła do drugiej płaszczyzny.

 Niech płaszczyzny prostopadłe

α i β przecinają się na prostej c, a prosta b w płaszczyźnie β jest prostopadła do prostej c i przecina ją w punkcie B (ryc. 425). Zgodnie z definicją

dzieląc prostopadłość płaszczyzn, w płaszczyźnie β prosta przechodzi przez punkt B

b 1, prostopadle do płaszczyzny α. Wiadomo, że jest prostopadła do prostej c. Ale co-

Jeśli przetniesz punkt na prostej w płaszczyźnie, możesz narysować tylko jedną prostą prostopadłą do danej prostej. Dlatego

linie b i b 1 pokrywają się. Oznacza to, że prosta jednej płaszczyzny, prostopadła do linii przecięcia dwóch prostopadłych płaszczyzn, jest prostopadła do drugiej płaszczyzny. ■

Zastosujmy rozważane twierdzenie do uzasadnienia innego znaku prostopadłości płaszczyzn, istotnego z punktu widzenia późniejszego badania względnego położenia dwóch płaszczyzn.

Niech płaszczyzny α i β będą prostopadłe, prosta c jest linią ich przecięcia. Przez dowolny punkt A rysujemy linię prostą c

w płaszczyznach α i β proste aib, prostopadłe do prostej c (ryc. 426). Według teorii

Me 2, proste a i b są prostopadłe odpowiednio do płaszczyzn β i α, zatem są do siebie prostopadłe: a b . Prosty

aib definiują pewną płaszczyznę γ. Linia przecięcia z płaszczyznami α i β

prostopadle do płaszczyzny γ, bazując na prostopadłości prostej i płaszczyzny (Twierdzenie 1 § 18): c a, c b, a γ, b γ. Jeżeli uwzględnimy dowolność wyboru punktu A na prostej c oraz fakt, że przez punkt A prostej c przechodzi jedna płaszczyzna prostopadła do niego, wówczas możemy wyciągnąć następujący wniosek.

Twierdzenie 3 (o płaszczyźnie prostopadłej do linii przecięcia płaszczyzn prostopadłych).

Płaszczyzna prostopadła do linii przecięcia dwóch prostopadłych płaszczyzn przecina te płaszczyzny wzdłuż prostopadłych prostych.

W ten sposób ustalono kolejną właściwość płaszczyzn prostopadłych. Właściwość ta jest charakterystyczna, to znaczy, jeśli jest prawdziwa dla jakichś dwóch płaszczyzn, to płaszczyzny są do siebie prostopadłe. Mamy jeszcze jeden znak prostopadłości płaszczyzn.

Twierdzenie 4 (drugie kryterium prostopadłości płaszczyzn).

Jeżeli bezpośrednie przecięcia dwóch płaszczyzn przez trzecią płaszczyznę prostopadłą do linii ich przecięcia są prostopadłe, to te płaszczyzny również są prostopadłe.

 Niech płaszczyzny α i β przecinają się na prostej z, a płaszczyzna γ, prostopadła do prostej z, przecina odpowiadające im płaszczyzny α i β

odpowiednio wzdłuż linii prostych a i b (ryc. 427). Według warunku a b . Ponieważ γ c, to a c. A zatem prosta a jest prostopadła do płaszczyzny β, zgodnie ze znakiem prostopadłości prostej i płaszczyzny (Twierdzenie 1 § 18). Otóż ​​to-

Tak, wynika z tego, że płaszczyzny α i β są prostopadłe, zgodnie ze znakiem prostopadłości płaszczyzn (Twierdzenie 1). ■

Na uwagę zasługują także twierdzenia o związkach między prostopadłością dwóch płaszczyzn trzeciej płaszczyzny a ich wzajemnym położeniem.

Twierdzenie 5 (o linii przecięcia dwóch płaszczyzn prostopadłych do trzeciej płaszczyzny).

Jeżeli przecinają się dwie płaszczyzny prostopadłe do trzeciej płaszczyzny, to linia ich przecięcia jest prostopadła do tej płaszczyzny.

 Niech płaszczyzny α i β, prostopadłe do płaszczyzny γ, przecinają się na prostej a (a || γ), a A jest punktem przecięcia prostej a z

Prostopadłość płaszczyzn
płaszczyzna γ (ryc. 428). Punkt A należy do
żyje wzdłuż linii przecięcia płaszczyzn γ i α, γ
i β oraz, pod warunkiem, α γ i β γ. Dlatego wg
wyznaczanie prostopadłości płaszczyzny
tey, przez punkt A możesz poprowadzić linie proste,
leżące w płaszczyznach α	i β i prostopadłe
płaszczyzny polarne γ. Bo przez punkt
można narysować tylko jedną linię prostą,
prostopadle do płaszczyzny, a następnie konstrukcję
linie proste pokrywają się i pokrywają się z linią
przecięcia płaszczyzn α i β. Zatem prosta a jest linią
przecięcie płaszczyzn α i β jest prostopadłe do płaszczyzny γ. ■

Rozważmy twierdzenie opisujące związek pomiędzy równoległością i prostopadłością płaszczyzn. Otrzymaliśmy już odpowiedni wynik dla linii prostych i płaszczyzn.

Twierdzenie 6 (o płaszczyznach równoległych prostopadłych do trzeciej płaszczyzny).

Jeżeli jedna z dwóch równoległych płaszczyzn jest prostopadła do trzeciej, to druga płaszczyzna jest do niej prostopadła.

 Niech płaszczyzny α i β będą równoległe, a płaszczyzna γ prostopadła do płaszczyzny α. Ponieważ płaszczyzna γ

przecina płaszczyznę α, to musi przecinać także płaszczyznę β równoległą do niej. Weźmy pro-

dowolną linię prostą m prostopadłą do płaszczyzny γ i przeciągnij przez nią, a także przez dowolny punkt płaszczyzny β, płaszczyznę δ (ryc. 429).

Płaszczyzny δ i β przecinają się na prostej n, a ponieważ α ║ β, to m ║ n (Twierdzenie 2 §18). Z Twierdzenia 1 wynika, że ​​n γ, a co za tym idzie, płaszczyzna β przechodząca przez prostą n będzie również prostopadła do płaszczyzny γ.

Udowodnione twierdzenie daje kolejny znak prostopadłości płaszczyzn.

Można narysować płaszczyznę prostopadłą do danego punktu przez dany punkt, korzystając ze znaku prostopadłości płaszczyzn (Twierdzenie 1). Wystarczy poprowadzić przez ten punkt linię prostą, prostopadłą do zadanej płaszczyzny (patrz zadanie 1 § 19). A następnie narysuj płaszczyznę przez zbudowaną linię prostą. Będzie ona prostopadła do zadanej płaszczyzny zgodnie z określonym kryterium. Jest oczywiste, że można narysować nieskończoną liczbę takich płaszczyzn.

Bardziej wymowny jest problem zbudowania płaszczyzny prostopadłej do danej, pod warunkiem, że przechodzi ona przez daną prostą. Wiadomo, że jeśli dana prosta jest prostopadła do danej płaszczyzny, to można skonstruować nieskończoną liczbę takich płaszczyzn. Pozostaje rozważyć przypadek, gdy dana prosta nie jest prostopadła do danej płaszczyzny. Możliwość takiej konstrukcji uzasadniona jest na poziomie modeli fizycznych linii prostych i płaszczyzn w przykładzie 1.

Zadanie 1. Udowodnić, że przez dowolną prostą, która nie jest prostopadła do płaszczyzny, można narysować płaszczyznę prostopadłą do danej płaszczyzny.

 Niech będzie dana płaszczyzna α i prosta l, l B\ a. Weźmy dowolny punkt M na linii l i narysuj przez niego linię m, prostopadłą do płaszczyzny α (ryc. 430, a). Ponieważ, zgodnie z warunkiem, l nie jest prostopadłe do α, wówczas linie l i m przecinają się. Za pomocą tych prostych można narysować płaszczyznę β (ryc. 430, b), która zgodnie z testem prostopadłości płaszczyzn (Twierdzenie 1) będzie prostopadła do płaszczyzny α. ■

Przykład 3. Przez wierzchołek A ostrosłupa foremnego SABC z podstawą ABC poprowadź linię prostą prostopadłą do płaszczyzny ściany bocznej SBC.

 Aby rozwiązać to zadanie, korzystamy z twierdzenia o prostopadłej do linii przecięcia płaszczyzn prostopadłych

(Twierdzenie 2). Niech K będzie środkiem krawędzi BC (ryc. 431). Płaszczyzny AKS i BCS są prostopadłe, zgodnie ze znakiem prostopadłości płaszczyzn (Twierdzenie 1). Rzeczywiście, BC SK i BC AK są jak środkowe narysowane do podstaw w trójkątach równoramiennych. Zatem zgodnie z kryterium prostopadłości prostej i płaszczyzny (Twierdzenie 1 §18) prosta BC jest prostopadła do płaszczyzny AKS. Płaszczyzna BCS przechodzi przez linię prostopadłą do płaszczyzny AKS.

Budowa. Narysujmy w płaszczyźnie AKS linię AL od punktu A, prostopadle do prostej KS – linii przecięcia płaszczyzn AKS i BCS (ryc. 432). Z twierdzenia o prostopadłości do linii przecięcia płaszczyzn prostopadłych (Twierdzenie 2) wynika, że ​​prosta AL jest prostopadła do płaszczyzny BCS. ■

	Pytania kontrolne
	Na ryc. 433 przedstawia kwadrat ABCD,
	linia MD jest prostopadła do płaszczyzny
	ABCD. Która z par samolotów nie jest
	są prostopadłe:
		MAD i MDC;		MBC i MAV;
		ABC i MDC;		MAD i MAV?

2. Na ryc. 434 jest wyświetlany poprawnie- nowa czworokątna piramida

SABCD, punkty P, M, N - środkowy -

Krawędzie AB, BC, BS, O są środkami podstawy ABCD. Która z par jest płaska- kości są prostopadłe:

1) ACS i BDS; 2) MOS i POS;

3) COS i MNP; 4) MNP i SOB;

5) CND i ABS?

		Prostopadłość prostych i płaszczyzn
3. Na ryc. 435	przedstawia prostokąt
trójkąt		z kątem prostym C i
prosta BP, prostopadła do płaszczyzny
ty ABC. Które z poniższych par są płaskie?
kości są prostopadłe:
1) CBP i ABC;		2) ABP i ABC;

3) PKA i PBC; 4) PAC i PAB?

4. Obie płaszczyzny są prostopadłe. Czy jest to możliwe poprzez dowolny punkt jednego z powinni narysować linię prostą w tej płaszczyźnie, drugiej płaszczyźnie?

5. Nie można narysować linii prostej w płaszczyźnie α, ale w płaszczyźnie β. Czy te samoloty mogą być moje?

6. Czy przez pewien punkt płaszczyzny α przechodzi w tej płaszczyźnie prosta i jest do niej prostopadła, tak że płaszczyzny α i β są prostopadłe?

Do słupka pionowego mocuje się odcinek ogrodzenia, czy można twierdzić, że płaszczyzna ogrodzenia jest pionowa?

Jak przymocować tarczę pionowo do szyny równoległej do powierzchni ziemi?

Dlaczego powierzchnia drzwi, niezależnie od tego, czy są zamknięte, czy otwarte, jest pionowa w stosunku do podłogi?

Dlaczego pion ściśle przylega do pionowej ściany, ale niekoniecznie do nachylonej?

Czy można przymocować tarczę do pochyłego słupa tak, aby była ona prostopadła do powierzchni ziemi?

Jak w praktyce określić, czy płaszczyzna jest prostopadła

ściany płaska podłoga? prostopadłe prostopadłe prostopadłe- prosto, w pozycji leżącej - β. Prawda 7. . Możliwe 8.9.10.11.12.

Ćwiczenia graficzne

1. Na ryc. 436 pokazuje sześcian ABCDA 1 B 1 Do 1 Re 1 .

1) Określ płaszczyzny prostopadłe do płaszczyzny VDD 1.

2) Jak tam samoloty i

A1 B1 KABINA 1 C 1

Prostopadłość płaszczyzn
			437 płaskich kwadratów ABCD i
	ABC1 D1		prostopadły. Dystans		CC1
	równa się b. Znajdź długość odcinka:
		AB;		D1C;
		D1D;		C1 D.	Dan-
	Zbuduj rysunek zgodnie z podanym
	1) Płaszczyzny trójkątów równobocznych
	ABC i ABC są prostopadłe.
		Płaszczyzna ABC jest prostopadła do płaszczyzn BDC i BEA.
		Płaszczyzny α i β są prostopadłe do płaszczyzny γ i przecinają się
	wzdłuż linii prostej a, linie ich przecięcia z płaszczyzną γ
	są liniami prostymi b i c.
		W prostokątnym równoległościanie ABCDA 1 B 1 C 1 D 1
	kości AB 1 C 1 i ICA 1 są prostopadłe.

421. Odcinek OS wykreślono ze środka O kwadratu ABCD prostopadle do jego płaszczyzny.

1°) Określ względne położenie płaszczyzn ACS

i ABC.

2°) Określ względne położenie płaszczyzn ACS

i BDS.

3) Skonstruuj płaszczyznę przechodzącą przez prostą OS prostopadłą do płaszczyzny ABS.

4) Skonstruuj płaszczyznę prostopadłą do płaszczyzny ABC i przechodzącą przez środki boków AD i CD.

422. Z punktu przecięcia O przekątnych rombu ABCD rysuje się odcinek OS prostopadle do płaszczyzny rombu; AB=DB=

1°) Określ względną pozycję SDB i

ABC, SDB i ACS.

2°) Skonstruuj płaszczyznę przechodzącą przez prostą BC, prostopadłą do płaszczyzny ABD.

3) Narysuj płaszczyznę prostopadłą do płaszczyzny ABC przechodzącą przez środek F odcinka CS.

4) Znajdź obszar trójkąta BDF.

423. Biorąc pod uwagę sześcian ABCDA1 B1 C1 D1.

1°) Określ względne położenie płaszczyzn AB 1 C 1

i CDD1.

2°) Określ względne położenie płaszczyzn AB 1 C 1

i CD1A1.

3°) Skonstruuj płaszczyznę przechodzącą przez punkt A, prostopadłą do płaszczyzny BB 1 D 1.

4) Skonstruuj odcinek sześcianu z płaszczyzną przechodzącą przez środki krawędzi A 1 D 1 i B 1 C 1 prostopadle do płaszczyzny ABC. 5) Określ względne położenie płaszczyzny AA 1 B i płaszczyzny przechodzącej przez środek żeber A 1 B 1, C 1 D 1, CD.

6) Znajdź pole przekroju sześcianu przez płaszczyznę przechodzącą przez krawędź BB 1 i środek krawędzi A 1 D 1 (BB ​​​​1 = a).

7) Skonstruuj punkt symetryczny do punktu A względem płaszczyzny A 1 B 1 C.

424. W czworościanie foremnym ABCD o krawędzi 2 cm punkt M jest środkiem odcinka DB, a punkt N środkiem odcinka AC.

1°) Udowodnij, że prosta DB jest prostopadła do płaszczyzny

2°) Udowodnij, że płaszczyzna BDM jest prostopadła do płaszczyzny AMC.

3) Przez punkt O przecięcia środkowych trójkąta ADC poprowadź linię prostą prostopadłą do płaszczyzny AMC.

4) Znajdź długość tego odcinka wewnątrz czworościanu. 5) W jakim stosunku płaszczyzna AMC dzieli ten odcinek?

425. Dwa trójkąty równoboczne ABC i ADC leżą w płaszczyznach prostopadłych.

1°) Znajdź długość odcinka BD, jeśli AC = 1 cm.

2) Udowodnij, że płaszczyzna BKD (K leży na prostej AC) jest prostopadła do płaszczyzny każdego z trójkątów wtedy i tylko wtedy, gdy K jest środkiem boku AC.

426. Prostokąt ABCD, którego boki wynoszą 3 cm i 4 cm, zakrzywiono wzdłuż przekątnej AC w ​​taki sposób, że trójkąty ABC i ADC leżą w płaszczyznach prostopadłych. Wyznacz odległość pomiędzy punktami B i D po zgięciu prostokąta ABCD.

427. Przez ten punkt narysuj płaszczyznę prostopadłą do każdej z dwóch podanych płaszczyzn.

428°. Udowodnić, że płaszczyzny sąsiednich ścian sześcianu są prostopadłe.

429. Płaszczyzny α i β są do siebie prostopadłe. Z punktu A płaszczyzny α poprowadzono prostą AB, prostopadłą do płaszczyzny β. Udowodnij, że prosta AB leży w płaszczyźnie α.

430. Udowodnij, że jeśli płaszczyzna i prosta nieleżąca w tej płaszczyźnie są prostopadłe do tej samej płaszczyzny, to są do siebie równoległe.

431. Przez punkty A i B leżące na linii przecięcia p płaszczyzn α i β prostopadłych do siebie, poprowadzono linie proste prostopadłe do p: AA 1 w α, BB 1 w β. Punkt X leży na prostej AA 1, a punkt Y na BB 1. Udowodnij, że prosta ВB 1 jest prostopadła do prostej ВХ, a prosta АА 1 jest prostopadła do prostej АY.

432*. Przez środek każdego boku trójkąta poprowadzono płaszczyznę prostopadłą do tego boku. Udowodnić, że wszystkie trzy narysowane płaszczyzny przecinają się wzdłuż jednej prostej prostopadłej do płaszczyzny trójkąta.

Ćwiczenia do powtórzenia

433. W trójkącie równobocznym z bokiem b określić: 1) wysokość; 2) promienie okręgów wpisanych i opisanych.

434. Z jednego punktu do danej linii poprowadzono prostą prostopadłą i dwie ukośne. Oblicz długość prostopadłych, jeśli nachylone wynoszą 41 cm i 50 cm, a ich rzuty na tę prostą wynoszą 3:10.

435. Określ ramiona trójkąta prostokątnego, jeśli bi- sectrix kąta prostego dzieli przeciwprostokątną na odcinki o długości 15 cm i

Podstawowa definicja

Nazywa się te dwa samoloty

są prostopadłe , jeśli każdy z nich jest utworzony przez linie proste- mi, prostopadle- mi drugiej płaszczyzny i przechodząca przez punkty przecięcia tych płaszczyzn.

	Główne stwierdzenia
Znak prostopadły		Jeśli sam
jasność		samoloty	przechodzić-
samoloty		przejdź przez
		prostopadły
		w takim razie drugi samolot		b α, b α β
		te samoloty są
		prostopadły.

		sięgacz-		dwa samoloty
otwór			są wówczas prostopadłe
skrzyżowaniasperpen			bezpośredni, należący do
dikularny		płaski	dzieląc jeden samolot
			i prostopadłe
				skrzyżowania
			te samoloty, per-		α β, b β, c = α ∩β,
			prostopadle do drugiego		b do b α
			samolot.

Artykuł ten poświęcony jest płaszczyznom prostopadłym. Definicje i oznaczenia zostaną podane wraz z przykładami. Sformułowany zostanie znak prostopadłości płaszczyzn i warunek jego spełnienia. Rozwiązania podobnych problemów zostaną omówione na przykładach.

Yandex.RTB R-A-339285-1

Jeżeli między przecinającymi się liniami istnieje kąt, możemy mówić o określeniu płaszczyzn prostopadłych.

Definicja 1

Pod warunkiem, że kąt między liniami prostopadłymi wynosi 90 stopni, nazywa się je prostopadły.

Oznaczenie prostopadłości zapisuje się zwykle znakiem „⊥”. Jeżeli warunek stwierdza, że ​​płaszczyzny α i β są prostopadłe, to zapis przyjmuje postać α ⊥ β. Poniższe zdjęcie pokazuje szczegółowo.

Jeżeli w chwycie podano, że płaszczyzny α i β są prostopadłe, oznacza to, że α jest prostopadłe do β i odwrotnie. Takie płaszczyzny nazywane są wzajemnie prostopadłymi. Na przykład ściana i sufit w pomieszczeniu są wzajemnie prostopadłe, ponieważ przecinając się, tworzą kąt prosty.

Prostopadłość płaszczyzn - znak i warunek prostopadłości

W praktyce można spotkać się z zadaniami, w których konieczne jest określenie prostopadłości danych płaszczyzn. Najpierw musisz określić kąt między nimi. Jeśli jest równy 90 stopni, wówczas z definicji uważa się je za prostopadłe.

Aby udowodnić prostopadłość dwóch płaszczyzn, stosuje się znak prostopadłości dwóch płaszczyzn. Sformułowanie zawiera pojęcia prostej prostopadłej i płaszczyzny. Dokładną definicję kryterium prostopadłości napiszmy w formie twierdzenia.

Twierdzenie 1

Jeżeli jedna z dwóch danych płaszczyzn przecina linię prostopadłą do drugiej płaszczyzny, to dane płaszczyzny są prostopadłe.

Dowód znajduje się w podręczniku geometrii dla klas 10-11, gdzie znajduje się szczegółowy opis. Ze znaku wynika, że ​​jeśli płaszczyzna jest prostopadła do linii przecięcia dwóch danych płaszczyzn, to jest prostopadła do każdej z tych płaszczyzn.

Istnieje warunek konieczny i wystarczający dowodu. Rozważmy je dla prostopadłości dwóch danych płaszczyzn, co służy do sprawdzenia ich prostopadłości, umieszczonej w prostokątnym układzie współrzędnych przestrzeni trójwymiarowej. Aby dowód był ważny, konieczne jest zastosowanie definicji wektora normalnego płaszczyzny, co pozwala wykazać warunek konieczny i wystarczający prostopadłości płaszczyzn.

Twierdzenie 2

Aby prostopadłość przecinających się płaszczyzn była oczywista, konieczne i wystarczające jest, aby wektory normalne danych płaszczyzn przecinały się pod kątem prostym.

Dowód

Niech zostanie określony prostokątny układ współrzędnych w przestrzeni trójwymiarowej. Jeśli mamy n 1 → = (A 1, B 1, C 1) i n 2 → = (A 2, B 2, C 2), które są wektorami normalnymi danych płaszczyzn α i β, to konieczny i wystarczający warunek prostopadłości wektorów n 1 → i n 2 → przyjmie postać

n 1 → , n 2 → = 0 ⇔ ZA 1 · ZA 2 + b 1 · B 2 + do 1 · do 2 = 0

Stąd otrzymujemy, że n 1 → = (A 1, B 1, C 1) i n 2 → = (A 2, B 2, C 2) są wektorami normalnymi danych płaszczyzn i dla rzeczywistości prostopadłości α i β jest to konieczne i wystarczające, aby iloczyn skalarny wektorów n 1 → i n 2 → był równy zeru i dlatego przybierał postać n 1 → , n 2 → = 0 ⇔ A 1 · A 2 + B 1 · B 2 + do 1 · do 2 = 0 .

Równość jest spełniona.

Przyjrzyjmy się bliżej przykładom.

Przykład 1

Wyznaczyć prostopadłość płaszczyzn określonych w prostokątnym układzie współrzędnych O x y z przestrzeni trójwymiarowej określonej równaniami x - 3 y - 4 = 0 i x 2 3 + y - 2 + z 4 5 = 1?

Rozwiązanie

Aby znaleźć odpowiedź na pytanie o prostopadłość, należy najpierw znaleźć współrzędne wektorów normalnych danych płaszczyzn, po czym można sprawdzić prostopadłość.

x - 3 y - 4 = 0 to ogólne równanie płaszczyzny, z którego można od razu przekształcić współrzędne wektora normalnego równe n 1 → = (1, - 3, 0).

Aby wyznaczyć współrzędną wektora normalnego płaszczyzny x 2 3 + y - 2 + z 4 5 = 1, przejdźmy od równania płaszczyzny w odcinkach do ogólnego.

Następnie otrzymujemy:

x 2 3 + y - 2 + z 4 5 ⇔ 3 2 x - 1 2 y + 5 4 z - 1 = 0

Następnie n 2 → = 3 2, - 1 2, 5 4 są współrzędnymi wektora normalnego płaszczyzny x 2 3 + y - 2 + z 4 5 = 1.

Przejdźmy do obliczenia iloczynu skalarnego wektorów n 1 → = (1, - 3, 0) i n 2 → = 3 2, - 1 2, 5 4.

Otrzymujemy, że n 1 → , n 2 → = 1 · 3 2 + (- 3) · - 1 2 + 0 · 5 4 = 3 .

Widzimy, że nie jest ono równe zeru, co oznacza, że ​​podane wektory nie są prostopadłe. Wynika z tego, że płaszczyzny również nie są prostopadłe. Warunek nie jest spełniony.

Odpowiedź: płaszczyzny nie są prostopadłe.

Przykład 2

Prostokątny układ współrzędnych O x y z ma cztery punkty o współrzędnych A - 15 4, - 7 8, 1, B 17 8, 5 16, 0, C 0, 0, 3 7, D - 1, 0, 0. Sprawdź, czy płaszczyzny A B C i A B D są prostopadłe.

Rozwiązanie

Najpierw musisz obliczyć iloczyn skalarny wektorów tych płaszczyzn. Jeśli jest równe zero, tylko w tym przypadku możemy uznać, że są one prostopadłe. Znajdujemy współrzędne wektorów normalnych n 1 → i n 2 → płaszczyzny A B C i A B D.

Z podanych współrzędnych punktów obliczamy współrzędne wektorów A B → , A C → , A D → . Otrzymujemy to:

ZA B → = 47 8, 19 16, - 1, ZA C → = 15 4, 7 8, - 4 7, ZA D → = 11 4, 7 8, - 1.

Wektor normalny płaszczyzny A B C jest iloczynem wektorowym wektorów A B → i A C →, a dla A B D iloczynem wektorowym A B → i A D →. Stąd to rozumiemy

n 1 → = ZA B → × A C → = ja → jot → k → 47 8 19 16 - 1 15 4 7 8 - 4 7 = 11 56 i → - 11 28 j → + 11 16 k → ⇔ n 1 → = 11 56 , - 11 28 , 11 16 n 2 → = ZA B → × A D → = ja → jot → k → 47 8 19 16 - 1 11 4 7 8 - 1 = - 5 16 ja → + 25 8 jot → + 15 8 k → ⇔ n 2 → = - 5 16 , 25 8 , 15 8

Zacznijmy szukać iloczynu skalarnego n 1 → = 11 56, - ​​​​11 28, 11 16 i n 2 → = - 5 16, 25 8, 15 8.

Otrzymujemy: n 1 → , n 2 → = 11 56 · - 5 16 + - 11 28 · 25 8 + 11 16 · 15 8 = 0 .

Jeśli jest równe zero, to wektory płaszczyzn A B C i A B D są prostopadłe, to same płaszczyzny są prostopadłe.

Odpowiedź: płaszczyzny są prostopadłe.

Można było podejść do rozwiązania inaczej i wykorzystać równania płaszczyzn A B C i A B D. Po znalezieniu współrzędnych wektorów normalnych tych płaszczyzn można by sprawdzić, czy spełniony jest warunek prostopadłości wektorów normalnych tych płaszczyzn.

Jeśli zauważysz błąd w tekście, zaznacz go i naciśnij Ctrl+Enter